¿Qué Es Una Matriz Triangular Superior? 31 Ejemplos

Si eres de los que se equivocan y llaman a la matriz triangular superior la inferior y viceversa, estás en el lugar apropiado. No te importe no eres el único, te lo voy a solucionar con trucos muy fáciles.

Preparado y preparada, vamos a ello.

Contenidos que vas a ver

¿Qué es una matriz triangular?

¿Cuándo hablamos de una matriz es triangular? ¿Cómo identificar una matriz triangular? buenas preguntas, una matriz triangular tiene que tener las siguientes características:

Ser una matriz cuadrada, es decir, que tenga el mismo número de filas que de columnas.

En segundo lugar identificar la diagonal principal de la matriz, recuerda que son todos los elementos que tienen la misma fila y columna a_ij

Ahora debes ver si todos los elementos que están por encima o por debajo de la diagonal principal son todos ceros. Te he puesto dos ejemplos, ¿por qué? más adelante te darás cuenta.

¿Cansado/a de luchar con conceptos confusos y ejemplos complicados? 😣 No te preocupes más. Explora nuestras detalladas explicaciones sobre las 🧩 propiedades de las matrices y despídete del estrés. 💡

Matriz triangular superior

Te puedes preguntar, ¿por qué tengo dos ejemplos? y ¿cómo los puedo diferenciar? muy bien preguntado. Es cierto que hay dos tipos de matrices triangulares y vamos a ver cuál es cada una de ellas.

Todas las matrices cuadradas que debajo de la diagonal principal tengan todos sus elementos ceros se les denomina matriz triangular superior
Un amigo

En esta imagen verás un ejemplo. La matriz triangular superior es la que está señalada con una flecha

Qué es una matriz triangular inferior

Si quieres saber qué es una matriz inferior y un ejemplo no tienes más que verlo en este artículo.

Todas las matrices cuadradas que por encima de la diagonal principal tengan todos sus elementos ceros se les denomina matriz triangular inferior
Un amigo

Aquí tienes un ejemplo de matriz triangular inferior, es la que tiene la flecha

¿Quieres ver cuándo una matriz es triangular superior e inferior en video? Solo tienes que hacer clic y disfrutar de ello

Ejemplos de matriz triangular

A continuación verás varios ejemplos que te van a aclarar este concepto de matrices

Ejemplo de matriz triangular superior 2×2

Debes diferenciar las matrices que son triangulares superiores de las que no son ni triangulares, por lo tanto, aquí tienes estos tres ejemplos:

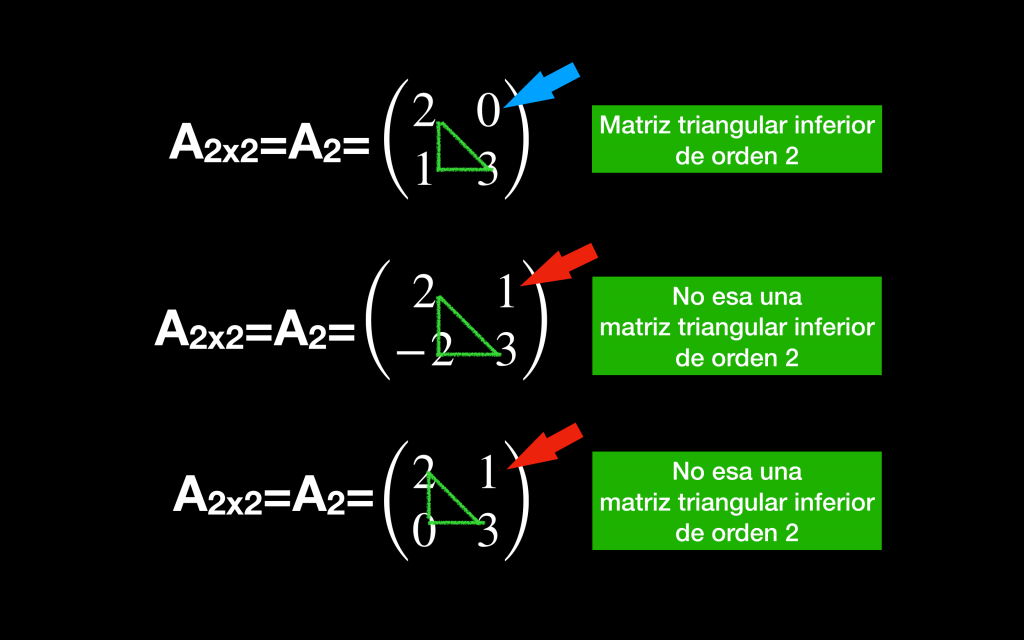
Ejemplo de matriz triangular inferior 2×2

Ahora toca las matrices inferiores.

Matriz triangular 4×4

Al aumentar el orden de las matrices se ve más claramente, fíjate:

¿Cómo hacer una matriz triangular?

Sí que se puede triangular una matriz cuadrada, pero con qué método. Yo te voy a dar el método más utilizado, que es realizando operaciones elementales entre las filas o el método de Gauss.

Te lo recuerdo brevemente lo que puedes hacer:

Cambiar filas de lugar.
Sustituir una fila por las operaciones elementales entre otras.
Puedes multiplicar una fila por un número, que no sea el 0.
Sumar filas.
Restar filas.
Hacer combinaciones lineales entre las filas.

¿Cómo hacer una matriz triangular superior?

Lo vas a ver desarrollado en este ejemplo, estate atento/a:

$\small \begin{pmatrix} 1 & 3 & -1\\ 2 & 2 & 3\\ 3 & -1 & 0 \end{pmatrix}\xrightarrow[F_{3}\rightarrow F_{3}-3F_{1}]{F_{2}\rightarrow F_{2}-2F_{1}}\begin{pmatrix} 1 & 3 & -1\\ 0 & -4 & 5\\ 0 & -10 & 3 \end{pmatrix}\newline\xrightarrow[]{F_{3}\rightarrow 4F_{2}-10F_{2}}\begin{pmatrix} 1 & 3 & -1\\ 0 & -4 & 5\\ 0 & 0 & -38 \end{pmatrix}$

¿Cómo hacer una matriz triangular inferior?

Bueno ahora es al revés pero no te preocupes que hay que resolver de la misma manera:

$\small \begin{pmatrix} 1 & 3 & -1\\ 2 & 2 & 3\\ 3 & -1 & 1 \end{pmatrix}\xrightarrow[F_{1}\rightarrow F_{1}+F_{3}]{F_{2}\rightarrow F_{2}-3F_{3}}\begin{pmatrix} 4 & 2 & 0\\ -7 & 5 & 0\\ 3 & -1 & 1 \end{pmatrix}\newline\xrightarrow[]{F_{1}\rightarrow 5F_{1}-2F_{2}}\begin{pmatrix} 34 & 0 & 0\\ -7 & 5 & 0\\ 3 & -1 & 1 \end{pmatrix}$

Determinante de este tipo de matrices

¿Cuál es el determinante de una matriz triangular superior e inferior? lo primero decirte que es igual cómo se calcula, tanto si es superior o inferior, por lo tanto, nos basaremos en una de ellas y punto.

Simplemente, el valor del determinante sale de multiplicar los elementos de la diagonal principal de la matriz. Te lo demuestro:

Aclaración: el determinante lo voy a desarrollar por menores complementarios, en concreto por el desarrollo de la primera columna
Un amigo

$\begin{vmatrix} a & b & c\\ 0 & d & e\\ 0 & 0 & f \end{vmatrix}=a\cdot \begin{vmatrix} d & e\\ 0 & f \end{vmatrix}-0\cdot \begin{vmatrix} b & c\\ 0 & f \end{vmatrix}-0\cdot \begin{vmatrix} b & c\\ d & e \end{vmatrix}=\newline =a\left ( df-0 \right )-0-0=adf$

Ejemplo:

$\begin{vmatrix} 1 & 3 & -1\\ 0 & 2 & 3\\ 0 & 0 & -2 \end{vmatrix}=1\cdot 2\cdot (-2)=-4$

Propiedades más importantes

Sí, por supuesto, tienen propiedades y las vas a ver.

Producto de matrices triangulares:

El producto de dos matrices triangulares superiores da como resultado otra matriz triangular superior.

$\begin{pmatrix} 1 & 2 & 3\\ 0 & -1 & -1 \\ 0 & 0 & 2 \end{pmatrix}\cdot \begin{pmatrix} -1 & 3 & 5\\ 0 & 2 & 2 \\ 0 & 0 & -3 \end{pmatrix}= \newline=\begin{pmatrix} -1 & 7 & 0\\ 0 & -2 & 1 \\ 0 & 0 & -6 \end{pmatrix}$

El producto de dos matrices triangulares inferiores da como resultado otra matriz triangular inferior.

$\begin{pmatrix} 2 & 0 & 0\\ -1 & -1 & 0 \\ 1 & 2 & 3 \end{pmatrix}\cdot \begin{pmatrix} -3 & 0 & 0\\ 2 & 2 & 0 \\ -1 & 3 & 5 \end{pmatrix}=\newline=\begin{pmatrix} -6 & 0 & 0\\ 1 & -2 & 0 \\ -2 & 13 & 15 \end{pmatrix}$

Traspuesta de una matriz triangular:

Recuerda que es cambiar filas por columnas, por lo tanto, pasamos de una matriz triangular superior a otra inferior y viceversa:

$\begin{pmatrix} 2 & 0 & 0 & 0\\ -1 & -1 & 0 & 0 \\ 1 & 2 & 3 & 0 \\ 1 & -2 & -3 & 3 \end{pmatrix}^{t}=\begin{pmatrix} 2 & -1 & 1 & 1\\ 0 & -1 & 2 & -2 \\ 0 & 0 & 3 & -3 \\ 0 & 0 & 0 & 3\end{pmatrix}$

¿Una matriz triangular es invertible?

Recuerda que para que una matriz tenga inversa se tiene que cumplir:

Que sea cuadrada
El determinante sea distinto de cero

Entonces las matrices cuadradas serán invertibles siempre y cuando no haya ningún cero en la diagonal principal de la matriz.

¿Cómo calcular los autovalores de una matriz triangular?

Los autovalores de las matrices triangulares coinciden con los elementos de la diagonal principal.

Ejemplo:

$\small \begin{vmatrix} 5 & 0 & 0\\ -1 & 2 & 0\\ 0 & 3 & -2 \end{vmatrix}\rightarrow \begin{vmatrix} 5-\lambda & 0 & 0\\ -1 & 2-\lambda & 0\\ 0 & 3 & -2-\lambda \end{vmatrix}=0\rightarrow \left ( 5-\lambda \right )\cdot \left ( 2-\lambda \right )\cdot \left ( -2-\lambda \right )=0$

$\small \left ( 5-\lambda \right )=0\rightarrow \lambda_{1} =5$

$\small \left ( 2-\lambda \right )=0\rightarrow \lambda_{2} =2$

$\small \left ( -2-\lambda \right )=0\rightarrow \lambda_{3} =-2$

Casos curiosos

Matriz diagonal

Recuerda que una matriz diagonal es aquella que los elementos que tiene por encima y por debajo de la diagonal principal son 0. Si te fijas en el siguiente ejemplo:

$\small \begin{pmatrix} 1 & 0 & 0\\ 0 & -2 & 0\\ 0 & 0 & 0 \end{pmatrix}$

¿Es superior o inferior? esto es lo curioso que puede ser a la vez triangular superior e inferior.

Matriz escalar

También le pasa a la matriz escalar (todos los elementos de la diagonal principal son iguales y el resto son ceros)

$\small \begin{pmatrix} 3 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 3 \end{pmatrix}$

Un caso particular es la matriz identidad

$\small \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$

Matriz nula

$\small \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}$

Es evidente que es un caso especial y curioso:

¡Descubre el Fascinante Mundo de las Matemáticas!

¿Quieres entender las matemáticas de una forma divertida y sencilla? 🚀 Visita nuestro canal de YouTube y encuentra videos llenos de trucos, explicaciones claras y ejemplos prácticos. ¡Aprende desde lo básico hasta lo avanzado con nosotros!

🔔 Suscríbete ahora y no te pierdas ninguna actualización. Cada semana subimos contenido nuevo que te ayudará a dominar las matemáticas paso a paso.

🎥 Mira nuestro último video y empieza tu aventura matemática hoy mismo!