Las 9 Propiedades De Los Radicales Más Importantes

Propiedades de los radicales: ¡multiplica por 5 tus conocimientos en radicales!

Raíces cuadradas

Raíces en forma de potencia

Multiplicación de radicales

División de raíces de cualquier índice

Y MUCHAS MÁS ¡QUÉDATE Y LO COMPRENDERÁS! SEGUIMOS

Contenidos que vas a ver

PROPIEDADES DE LAS RAÍCES CUADRADAS

Empezamos con los radicales de índice menor y los más usuales para luego dar el paso a radicales de mayor índice…Y más difíciles 🤦‍♀️➜ NO PASA NADA, APRENDERÁS.

¿Cuáles son las propiedades de las raíces cuadradas?

Te voy a dar una serie de definiciones que luego te van a ayudar a entender mejor los radicales de índice superior.

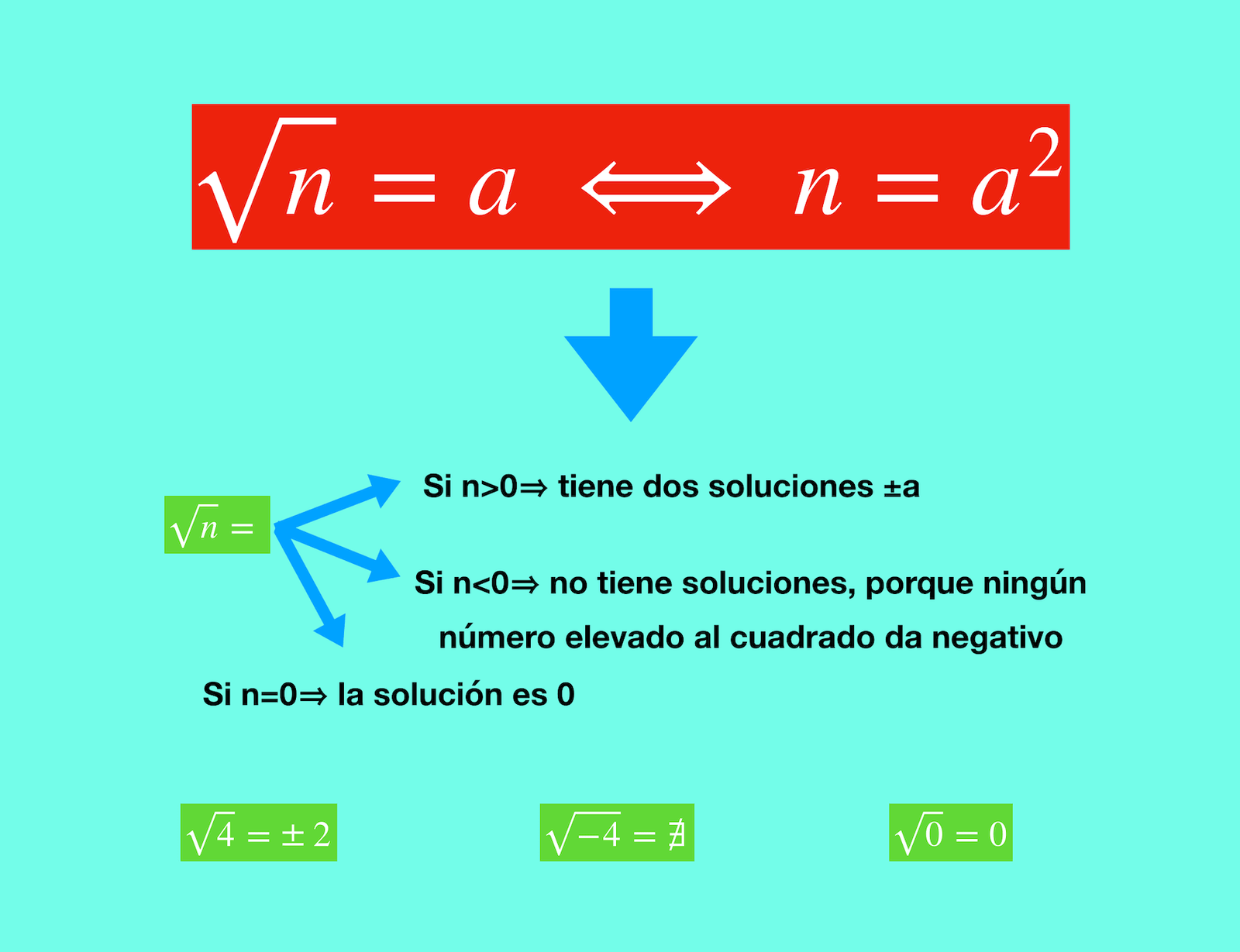
⬅︎¡¡¡ATENCIÓN, ANTES DE NADA!!!

Expresa en forma de potencia una raíz cuadrada

$propiedades de los radicales, cómo pasar a exponente fraccionario$

POTENCIA DE UNA RAÍZ CUADRADA

Cómo se suman las raíces cuadradas.

Siempre se pueden sumar raíces cuadradas 👏👏👏 Pero ¿cómo?…Simplemente la raíz resultante tiene el mismo radicando y el mismo índice y lo que se suma son los coeficientes que acompañan a las raíces cuadradas.

Ejemplo

$3\sqrt{2}+5\sqrt{2}=7\sqrt{2}$

$3\sqrt{2}-5\sqrt{2}=-2\sqrt{2}$

$3\sqrt{3}+5\sqrt{2}=$ no se pueden sumar las raíces cuadradas.

Vas a ver muchos ejemplos explicados paso a paso al final de esta página, PERO VAS A IR POCO A POCO

Propiedad de los radicales sobre la multiplicación de raíces cuadradas

A continuación, vas a ver cómo se multiplican radicales del mismo índice:

División de raíces cuadradas, esta propiedad de las raíces debes conocerla

Debes tener en cuenta que se dividen los coeficientes de los radicales y por otra parte los radicandos.

Y dentro de este contenido, para ti es de gran valor entender la racionalización de radicales, en este enlace aprendes sobre racionalizar, pero debes aumentar tus conocimientos en el mundo de los números r

canal de youtube sobre matemáticas, @masmath

¡Descubre las matemáticas en nuestro canal de YouTube! 🌟 Aprende trucos, resuelve problemas paso a paso y domina conceptos clave con nuestros vídeos fáciles de seguir. 🚀 Haz clic aquí y empieza a disfrutar de las matemáticas de forma sencilla y divertida. ¡Te esperamos! 🎓📚

PROPIEDADES DE LOS RADICALES DE CUALQUIER ÍNDICE

Pasamos ya a ver propiedades radicales con cualquier índice, te voy a dar las distintas propiedades con ejemplos aclaratorios de cada una de ellas. ¡Vamos a ello! 🤪

Expresa una raíz en forma de potencia

$propiedades de las raíces, en concreto pasar a exponente fraccionario. Estos radicales son de cualquier índice$

FÍJATE BIEN EN LAS LETRAS n y b, CÓMO PASAN DE UN LUGAR A OTRO, ESTA ES LA CLAVE

Multiplicación de raíces de igual índice

Mira siempre los índices, si son iguales, adelante. Fíjate en la imagen

¿Cómo se multiplica un número entero con una raíz? esta propiedad de la raíz no la sabías

¡¡¡FÍJATE EN EL ERROR!!!

¿Cómo se multiplican radicales con coeficientes?

CADA ELEMENTO VA POR SU LADO, CUIDADO

División de raíces de igual índice. Esta propiedad de los radicales de 4º ESO

ÍNDICES DE LOS RADICALES IGUALES, PUEDES OPERAR LA DIVISIÓN

Raíz de raíz

NUNCA APLIQUES ESTA PROPIEDAD DE LOS RADICALES SI HAY ALGUNA EXPRESIÓN ENTRE LOS RADICALES

Potencia de un radical

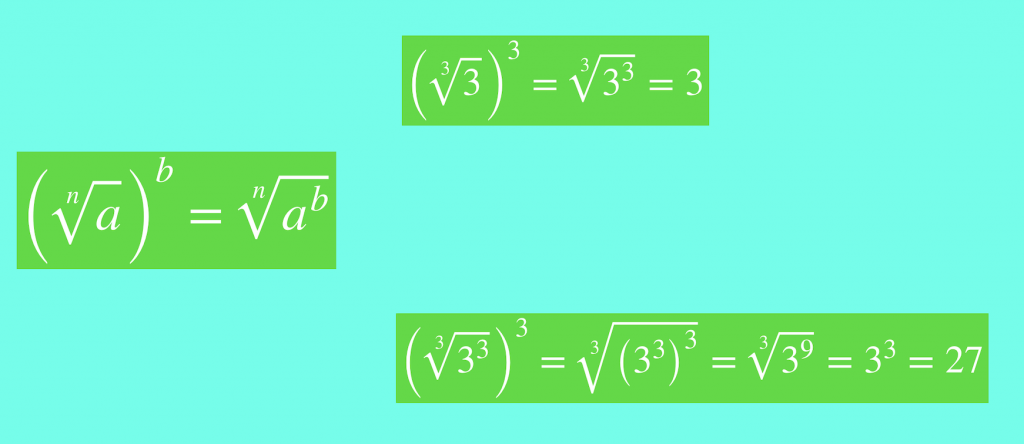
FÍJATE BIEN EN LA b

MÁS PROPIEDADES DE LAS RAÍCES

Todas estas preguntas están relacionadas con las propiedades de las raíces, ¿qué es la propiedad raíz de un producto? ¿cuáles son las propiedades de las raíces? ¿cuántas propiedades tienen las raíces? ¿qué son las leyes y propiedades de los radicales?

Para contestarte a estas preguntas y otras debes aprender bien las anteriores y las que vienen a continuación:

Simplificar radicales

Para simplificar los radicales debes saber que los nuevos radicales son equivalentes a los primeros y ¿cómo puede hacer estos radicales equivalentes?

Mira debes buscar el MCD, es decir, el máximo común divisor del índice y del exponente del radicando, lo voy a aplicar a este ejemplo:

$\sqrt[8]{5^{6}}=\sqrt[4]{5^3}$ como el MCD entre 8 y 6 es 2, lo que hago es dividir el índice entre 2 y me da 4 en el nuevo radical y también divido el exponente del radicando entre 2 y me da 3.

Pero, ¿se puede siempre obtener un radical equivalente a otro por simplificación? pues va a ser que NOOOOO.

Mira estos ejemplos:

$\sqrt[8]{5^3}$ como puedes comprobar el 8 y el 3 no tienen ningún divisor en común, distinto de 1, por lo que no puedes simplificar este radical.

$\sqrt[8]{5^2\cdot 2^5}$ en este caso tienes dos factores en el radicando, entre 8 y 2 el MCD es 2, pero entre 8 y 5 no hay MCD distinto de 1, por lo que no se puede hacer, es decir, que si puedes simplificar es porque puedes hacerlo en todo el radicando.

En este mismo apartado te voy a hablar de la amplificación de radicales, en este caso lo puedes hacer siempre, siempre puedes amplificar un radical…¿cómo?

Simplemente multiplica el índice y el exponente o los exponentes del radicando o de los radicandos por un mismo número natural.

$\sqrt[3]{4^2\cdot 3^5}=\sqrt[3\cdot 3]{4^{\left ( 2\cdot 3 \right )}\cdot 3^{\left ( 5\cdot 3 \right )}}= \sqrt[9]{4^6\cdot 3^{15}}$

Introducir factores dentro de un radical

¡¡¡CUIDADO!!! Recuerda que factores en matemáticas es alguna expresión que se multiplica, me explico, debes multiplicar el exponente de cada factor por el índice del radical, FÍJATE EN EL EJEMPLO

$ab^{2}c^{4}\sqrt[3]{a}=\sqrt[3]{a\cdot a^{3}\cdot b^{6}\cdot c^{12} }=\ raíz cuadrada[3]{a^{4}\cdot b^{6}\cdot c^{12}}$

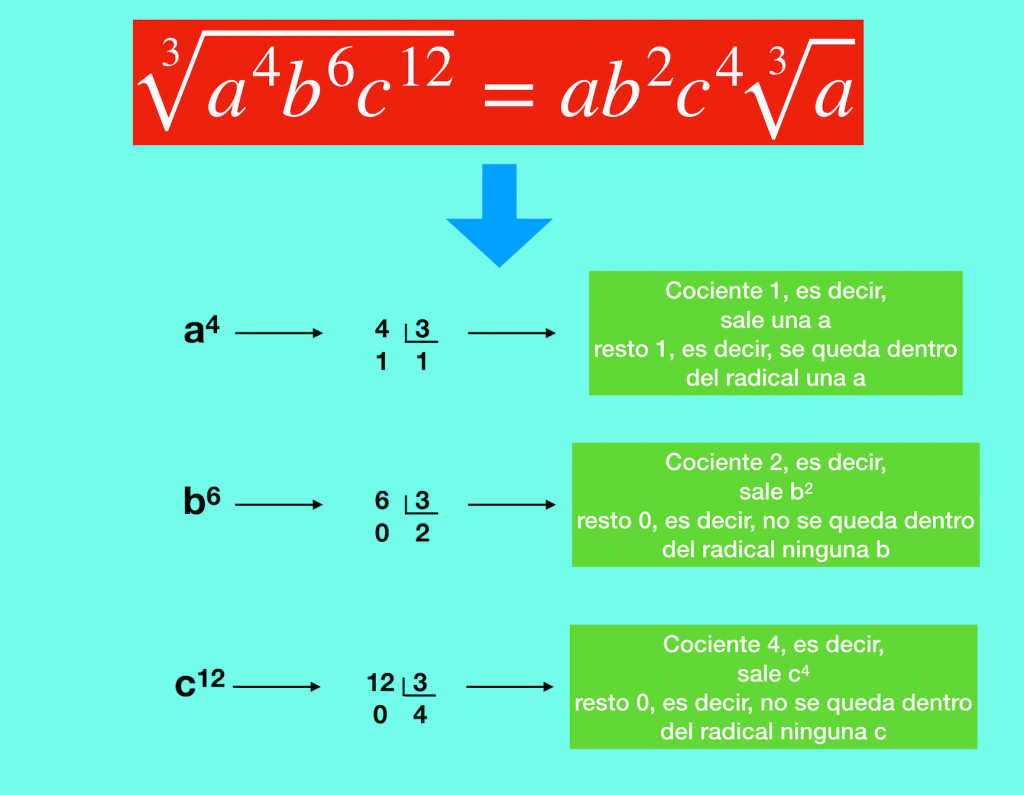
Extraer factores fuera del radical

¡¡¡NO PUEDES HACERLO SIEMPRE!!!

¿Quieres aprender?, pues mira el ejemplo anterior le vamos a dar la vuelta, es decir, vamos a ir desde el final al principio.

Solo lo puedes hacer si solo hay factores en el radicando.
Divide el exponente de cada factor entre el índice del radical.
El cociente te indicará el número de factores que salen fuera del radical.
El resto te informa de todos los factores que quedan dentro del radical.
Todos los factores que salgan fuera deben estar multiplicados.

La propiedad de la suma y la resta de radicales

¿Se pueden sumar o restar radicales?… SÍ

¿Siempre?…NO

🙀

¿Cuándo se pueden sumar o restar radicales?…Cuando los radicandos de los distintos radicales son iguales y los índices también

Pero, ¿cómo se suman o se restan?…Muy fácil, lo único que tienes que hacer es sumar o restar los coeficientes de los radicales y el radical se queda igual:

$2\sqrt{3}+4\sqrt{3}=6\sqrt{3}$

PROPIEDADES DE LOS RADICALES PDF

¿Cuántas y cuáles son las propiedades de la radicación?

Tanto si eres profesor como si eres alumno aquí tienes un pdf guía que te va a ayudar a tenerlo todo a mano estas propiedades de los radicales

¡¡¡CLICA AQUÍ Y LA CONSEGUIRÁS GRATIS!!!

PROPIEDADES DE LOS RADICALES 3º ESO

Si eres alumno de 3º ESO o tienes unos 13, 14 años este pdf te resume lo más importante de las propiedades de radicales.

¡¡¡AQUÍ LO TIENES GRATIS!!!

¿CUÁLES SON LAS PROPIEDADES DE LOS RADICALES CON EJEMPLOS?

¿Qué es radicación, propiedades y ejemplos? Lo que vas a ver en este apartado son ejemplos para que aprendas a aplicar las distintas propiedades de los radicales que hemos ido viendo.

SÍGUEME CON ESTAS PROPIEDADES DE LOS RADICALES

Simplificación de radicales

$\dpi{120} \large \sqrt[6]{b^{3}}=\sqrt{b}$
$\dpi{120} \large \sqrt[12]{1024}=\sqrt[12]{2^{10}}=\sqrt[6]{2^{5}}$
$\dpi{120} \large \sqrt[33]{b^{6}}=\sqrt[11]{b^{2}}$
$\dpi{120} \large \sqrt[10]{243a^{5}b^{15}c^{10}}=\sqrt[10]{3^{5}a^{5}b^{15}c^{10}}$
$\dpi{120} \large =\sqrt{3ab^{3}c^{2}}$

Extraer factores

$\dpi{120} \small \sqrt{98a^{2}bc^{4}}=\sqrt{3^{4}a^{2}bc^{4}}=3^{2}ac^{2}\sqrt{b}$
$\dpi{120} \small \sqrt[3]{81}=\sqrt[3]{3^{4}}=3\sqrt[3]{3}$
$\dpi{120} \small \sqrt{180}=\sqrt{2^{2}3^{2}5}=2\cdot 3 \sqrt{5}=6\sqrt{5}$
$\dpi{120} \small \sqrt{a^{3}b49}=7a\sqrt{ab}$

Simplificar y extraer

$\dpi{120} \small \sqrt[6]{m^{2}n^{6}}=\sqrt[3]{mn^{3}}=n\sqrt[3]{m}$
$\dpi{120} \small \sqrt[7]{7a^{14}b^{10}z^{7}}=a^{2}bz\sqrt[7]{7b^{3}}$
$\dpi{120} \small \sqrt{16a^{2}b^{6}}=4ab^{3}$
$\dpi{120} \small \sqrt[6]{19683y^{3}}=\sqrt[6]{3^{9}y^{3}}=\sqrt{3^{3}y}$
$\dpi{120} \small =3\sqrt{3y}$

Introducir factores

$\dpi{120} \grande 4\sqrt{5}=\sqrt{4^{2}5}=\sqrt{80}$
$\dpi{120} \large 3\sqrt[3]{7}=\sqrt[3]{3^{3}\cdot 7}=\sqrt{189}$
$\dpi{120} \large ab\sqrt[4]{5}=\sqrt[4]{5a^{4}b^{4}}$
$\dpi{120} \large 2\sqrt[6]{30}=\sqrt[6]{2^{6}\cdot 30}=\sqrt[6]{1920}$

Producto y cociente

$\dpi{120} \small \sqrt[3]{3}\cdot \sqrt[3]{7}=\sqrt[3]{3\cdot 7}=\sqrt[3]{21}$
$\dpi{120} \small \sqrt[5]{8}\sqrt[5]{3}= \sqrt[5]{8}\sqrt[5]{3}=\sqrt[5]{24}$
$\dpi{120} \small \sqrt{a^{5}}\sqrt{ab^{3}}=\sqrt{a^{6}b^{3}}=a^{3}b\sqrt{b}$
$\dpi{120} \small \sqrt{\frac{3}{5}}\sqrt{\frac{6}{7}}=\sqrt{\frac{3}{5}\cdot \frac{6}{7}}=\sqrt{\frac{18}{35}}$
$\dpi{120} \small \frac{\sqrt{50}}{\sqrt{2}}=\sqrt{\frac{50}{2}}=\sqrt{25}=5$
$\dpi{120} \small \sqrt{x^{3}y^{3}}:\sqrt{xy}=\sqrt{\frac{x^{3}y^{3}}{xy}}$
$\dpi{120} \small =\sqrt{x^{2}y^{2}}=xy$
$\dpi{120} \small \sqrt[4]{5^{2}\cdot 3^{3}}:\sqrt[4]{3}=\sqrt[4]{\frac{5^{2}\cdot 3^{3}}{3}}=\sqrt[4]{5^{2}\cdot 3^{2}}$
$\dpi{120} \small =\sqrt{25\cdot9}=\sqrt{225}$
$\dpi{120} \small \sqrt{\frac{3}{5}}:\sqrt{\frac{5}{3}}=\sqrt{\frac{3}{5}:\frac{5}{3}}=\sqrt{\frac{15}{15}}=1$

Potencia y raíz

$\dpi{120} \small \left (\sqrt[3]{2} \right )^{5}=\sqrt[3]{2^{5}}=2\sqrt[3]{2^{2}}$
$\dpi{120} \small \left (-3\sqrt{3} \right )^{3}=-27\sqrt{3^{3}}=-81\sqrt{3}$
$\dpi{120} \small \left (a\sqrt[4]{a^{2}b} \right )^{3}=a^{3}\sqrt[4]{a^{6}b^{3}}=a^{4}\sqrt[4]{a^{2}b^{3}}$
$\dpi{120} \small \left (\sqrt[6]{2^{4}} \right )^{4}=\sqrt[6]{2^{16}}=2^{2}\sqrt[6]{2^{4}}$
$\dpi{120} \small =4\sqrt[3]{2^{2}}$
$\dpi{120} \small \sqrt{\sqrt[3]{x}}=\sqrt[6]{x}$
$\dpi{120} \small \sqrt[5]{\sqrt[a]{6}}=\sqrt[5a]{6}$
$\dpi{120} \small \left (\sqrt{\sqrt{\sqrt{a}}}\right )^{7}=\sqrt[8]{a^{7}}$
$\dpi{120} \small \sqrt{\sqrt[3]{a\sqrt[5]{a}}}=\sqrt[6]{a\sqrt[5]{a}}=\sqrt[6]{^{\sqrt[5]{a^{5}a}}}$
$\dpi{120} \small =\sqrt[30]{a^{6}}=\sqrt[5]{a}$

Suma y resta

$\dpi{120} \small \sqrt{3}+6\sqrt{3}-\sqrt{3}+2\sqrt{3}$
$\dpi{120} \small =\left ( 1+6-1+2 \right )\sqrt{3}=8\sqrt{3}$
$\dpi{120} \small 7\sqrt{2}+\sqrt{3}-\sqrt{2}+5\sqrt{3}=$
$\dpi{120} \small =\left(7-1\right)\sqrt{2}+\left(1+6\right)\sqrt{3}=$
$\dpi{120} \small =6\sqrt{2}+7\sqrt{3}$
$\dpi{120} \small \sqrt{18}+\sqrt{50}-\sqrt{2}-\sqrt{32}=$
$\dpi{120} \tiny =\sqrt{3^{2}\cdot 2}+\sqrt{5^{2}\cdot 2}-\sqrt{2}-\sqrt{2^{5}}=$
$\dpi{120} \small =3\sqrt{2}+5\sqrt{2}-\sqrt{2}-2^{2}\sqrt{2}=$
$\dpi{120} \small =\left ( 3+5-1-4 \right )\sqrt{2}=3\sqrt{2}$

PREGUNTAS FRECUENTES SOBRE RADICALES PROPIEDADES

¿Qué son las propiedades de los radicales?

✳️ Herramienta matemática relacionada con los radicales que nos permiten resolver ejercicios donde haya raíces de cualquier índice.
✳️ Gracias a ellas los problemas sobre radicales son más fáciles de resolver

¿Cuáles son las propiedades de los radicales?

Las propiedades de los radicales son:

🌀 Radicales en forma de potencia.
🌀 Suma o resta de radicales.
🌀 Multiplicación de raíces de cualquier índice.
🌀 Cómo racionalizar radicales. Casos

¿Cuántas son las propiedades de la radicación?

Las propiedades de las raíces abarcan desde su forma potencial, con exponente fraccionario, hasta las operaciones básicas con los radicales, pasando por el tema principal que es la racionalización.

¿Qué son las leyes y propiedades de los radicales?

Son herramientas de las matemáticas que nos ayudan a solucionar ejercicios y problemas relacionados con los radicales ✅ Estas propiedades son importantísimas para facilitar el cálculo matemático de las raíces de cualquier índice.

TE PUEDE INTERESAR:

ANÁLISIS MATEMÁTICO

DERIVADAS

INTERVALOS