4 Tabla De Derivadas Gratis Para Ti

La tabla de derivadas inmediatas te va a ayudar a solucionar tu problema:

🔺 Aprenderás desde las más sencillas derivadas a las más complejas.
🔻 Calcularás la derivada de funciones.
🔸 Entenderás cómo derivar una función trigonométrica.
🔷 Y mucho más.

operaciones con funciones, propiedades de derivadas, derivadas propiedades, propiedades derivada

Contenidos que vas a ver

Tabla de derivadas inmediatas con ejercicios resueltos.

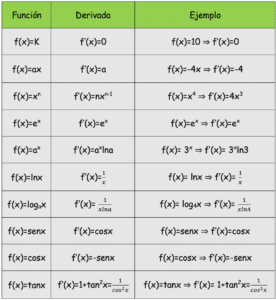
Aquí tienes la tabla de derivadas inmediatas, donde la función solo es x, atento a la simbología, f(x) es la función que hay que derivar, f'(x) es ya la función derivada, la e es el símbolo de la exponencial, ln del logaritmo neperiano, sen, cos y tan corresponde al seno, coseno y la tangente.

Aquí están tus derivadas pdf 1º bachillerato

Tabla de derivadas de funciones compuestas

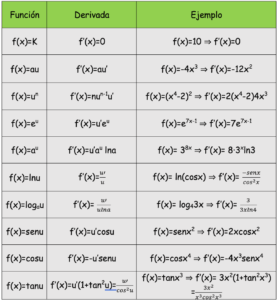
Esta otra tabla es la misma que la anterior pero la función es cualquier otra y la designo con u. Mira los ejercicios resueltos, te interesan bastante, tabla de derivadas directas.

Solo funciones trigonométricas. Aquí tienes información al respecto ⬇︎⬇︎⬇︎

📚 Las funciones trigonométricas son esenciales en matemáticas. Descubre más en nuestra tabla de derivadas de funciones trigonométricas.

¡¡¡ATENCIÓN!!!

Tratando este tema te recomiendo que no olvides que las normas de derivación que estás viendo por sí solas, no te va a servir para mejorar tus conocimientos sobre la teoría de las derivadas ¡CLICLA!

Tabla de operaciones con derivadas

Estas operaciones entre funciones y para resolver las derivadas te va a ser muy útil

Tabla de derivadas pdf

¿Problemas con las derivadas? Nuestras tablas simplifican el proceso y garantizan precisión. ¡Empieza a utilizarlas hoy! 📈🔍

Aquí vas a encontrar una tabla de derivadas completa para imprimir en pdf

Cómo calcular derivadas con la tabla de funciones derivadas

¿Cuáles son las fórmulas para calcular derivadas? Ya has visto las tablas de derivadas, ahora te voy a dar más ejercicios desarrollando cada fórmula de la tabla de derivadas

Derivada de una constante

$\bg_red \fn_jvn \LARGE f(x)=8\rightarrow f'(x)=0$

Derivada de x

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=x\rightarrow f'(x)=1$

Derivada de un polinomio de primer grado

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=2x+1\rightarrow f'(x)=2$

Derivada de una potencia

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=2x^{3}\rightarrow f'(x)=6x^{2}$

Derivada de una raiz

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=\sqrt[4]{3x}\rightarrow f'(x)=\frac{3}{4\sqrt[4]{\left ( 3x \right )^{3}}}$

Derivada de la suma de funciones

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=x^{2}+cosx\rightarrow\newline f'(x)=2x-senx$

Derivada de una constante por una función

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=7senx\rightarrow f'(x)=7cosx$

Derivada de un producto de funciones

$\small \bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=cosxsenx\rightarrow \newline f'(x)=-senxsenx+cosxcosx=\newline=-sen^{2}x+cos^{2}x$

Derivada de una constante dividida por una función

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=\frac{8}{x^{2}}\rightarrow f'(x)=\frac{-8\cdot 2x}{x^{4}}=\frac{-16}{x^{3}}$

Derivada de un cociente

$\small \bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=\frac{2x}{tgx} \newline \rightarrow f'(x)=\frac{2tgx-2x(1+tg^{2}x)}{tg^{2}x}$

Derivadas exponenciales

Derivada de la función exponencial de base un número distinto de e

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=4^{x^{2}}\rightarrow f'(x)=2x\cdot 4^{x^{2}}ln4

Derivada de la función exponencial de base e

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=e^{senx} \newline \rightarrow f'(x)=cosx\cdot e^{senx}$

Derivadas logarítmicas

Derivada del log neperiano

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=log_{4}\left ( x^{2}-2 \right )\rightarrow f'(x)=\frac{2x}{\left ( x^{2}-2 \right )ln4}

Derivada de un logaritmo en base a, distinta de e

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=lnsenx\rightarrow f'(x)=\frac{cosx}{senx}=cotgx

Derivadas trigonométricas

Derivada del seno de una función

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=senx^{2}\rightarrow f'(x)=2xcosx^{2}

Derivada del coseno de una función

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=cosx^{2}\rightarrow f'(x)=-2xsenx^{2}

Derivada de la tangente de una función

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=tg\left ( 2x+1 \right )\rightarrow f'(x)=1+tg^{2}\left ( 2x+1 \right )

Derivada de la cotangente

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=cotg8x\rightarrow f'(x)=\frac{-8}{sen^{2}8x}

Derivada de la secante

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=sec(3x-2)\rightarrow f'(x)=\frac{3sen\left ( 3x-2 \right )}{cos^{2}\left ( 3x-2 \right )}

Derivada de la cosecante

\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=cosecx^{3}\rightarrow f'(x)=\frac{-3x^{2}cosx^{3}}{sen^{2}x^{3}}

Derivadas trigonométricas inversas

$\small \bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=x^{2}+cosx\rightarrow \newline f'(x)=2x-senx$ Derivada del arcoseno

o derivada de arcoseno

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arcsenx^{2} \newline \rightarrow f'(x)=\frac{2x}{\sqrt{1-\left ( x^{2} \right )^{2}}}$

Derivada del arcocoseno

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arccosx^{2} \newline \rightarrow f'(x)=\frac{-2x}{\sqrt{1-\left ( x^{2} \right )^{2}}}$

Derivada del arcotangente

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arctg\left ( \frac{1}{x} \right ) \newline \rightarrow f'(x)=\frac{\frac{-1}{x^{2}}}{1+\left ( \frac{1}{x} \right )^{2}}$

Derivada del arcocontangente

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arccotg3x \newline \rightarrow f'(x)=\frac{-3}{1+\left ( 3x \right )^{2}}$

Derivada del arcocosecante

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arccosec(lnx) \newline \rightarrow f'(x)=\frac{-\frac{1}{x}}{lnx\sqrt{ln^{2}x-1}}$

Derivada del arcosecante

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=arcsec\left ( e^{x} \right ) \newline \rightarrow f'(x)=\frac{e^{x}}{e^{x}\sqrt{\left ( e^{x} \right )^{2}-1}}= \newline =\frac{1}{\sqrt{e^{2x}-1}}$

Derivada de una función elevada a otra función

$\inline \fn_jvn \LARGE f(x)=u^{v}\rightarrow f'(x)=v\cdot u^{v-1}\cdot u'+u^{v}\cdot v'\cdot lnu$

Ejemplo

$\bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE \bg_red \fn_jvn \LARGE f(x)=cosx^{lnx}\rightarrow f'(x)=lnx\cdot cosx^{lnx-1}\left ( -senx \right )+cosx^{lnx}\cdot \frac{1}{x}lnxcosx$